实时渲染中的软阴影技术
本文描述的是基于Shadow Mapping的软阴影技术,读者应该对Shadow Mapping 有基本的理解。
关于阴影走样
Shadow Mapping 有一个严重的问题就是阴影走样(Aliasing),这一点在我的渲染器CanvasToy上也非常明显
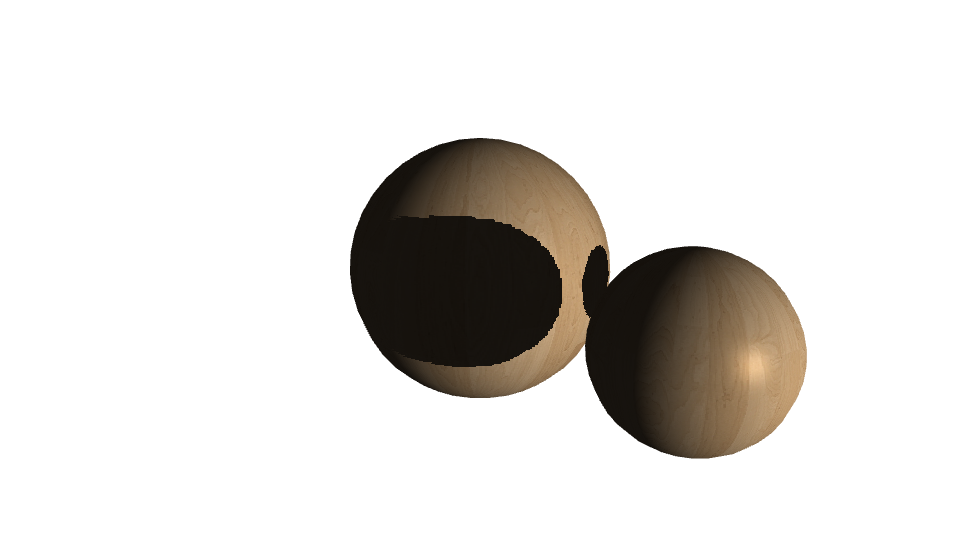
图中阴影边缘明显的锯齿就是阴影走样
阴影走样为什么会产生?以聚光灯为例,如果光源和遮挡物离场景很远,假设阴影纹理大小为1024*1024。当我们对场景中的一点找到对应shadow map中的深度,我们会在很大的矩形范围内得到同样的z(p)值,这样就形成了锯齿。
除了锯齿的问题,我们发现无论遮挡物有多远,阴影的边界依然很明显,这就是所谓的硬阴影。
综上,我们需要解决两个问题锯齿和明显的阴影边界。
为了更好地分析问题,我们定义一个shadow test function $$ s(x) = f(d(x), z(p)) $$ \(x\)是摄像机看到的场景中某一点,\(d(x)\) 是这一点到光源的距离,p是在阴影纹理中遮挡物的位置,z则是遮挡物的深度。 显然,对于标准阴影贴图技术 $$ f(d, z) = \begin{cases} 1, d < z \ 0, d \geq z \end{cases} $$
这个函数是离散的,我们希望对这个函数做一个变换,使其连续化。 我们可以直接对\(f(d, z)\)滤波,达到连续化的目的,然而这样的操作效率并不高,我们希望先一步对z进行滤波处理,这样我们就能在shadow pre-pass阶段进行滤波,不用在光照计算阶段进行重复的fetching和计算(这样效率很低)。 但是如果我们真的直接对z滤波,我们得不到想要的结果。原因很简单:,对\(f(d, z)\)滤波和对\(z\)滤波是完全不一样的,这里的\(f(d, z)\)是一个阶跃函数,由卷积定理,下面的式子不成立: $$ w \ast f(d(x), z) \neq f(d(x),(w*z)(p)) $$ 因此,我们看起来只能从\(f(d, z)\)入手,但是有些方法可以先把\(f(d, z)\)稍微变换一下,使其能满足卷积定理,从而应用pre-filtering
软阴影算法概览
软阴影主要解决两个问题,1:如何高效的blur,也就是如何生成一致的软阴影 2:如何利用距离控制阴影软硬程度,并与1中的算法结合
一致性软阴影:
-
Percentage-Closer Filter (PCF) PCF是直接对\(f(d, z)\)滤波的方法,效率相对较低
-
Variance Shadow Mapping (VSM) VSM巧妙地利用了切比雪夫不等式,\(f(d,z)\)是一个单边的近似公式,在这种情况下,对z进行pre-filter的效果是可以接受的
-
Convolution Shadow Mapping (CSM) CSM把\(f\)变成傅里叶级数求和的形式,从而得到一系列函数的和,对这些函数就有可能应用pre-filtering
-
Exponential Shadow Mapping (ESM) ESM相当简洁,使用的是一个单边指数函数来近似,效率和空间都要好的多,支持pre-filtering
距离相关的阴影: 这个方面最著名的是Percentage-Closer Soft Shadows (PCSS)
本文将逐一介绍这些技术
PCF滤波
既然要模糊阴影边缘,那我们就可以利用多重采样和插值函数,并将插值的结果作为\(f(d, z)\)的值。 这样,在阴影的边缘,离阴影越远的未被阴影照射到的部分采样结果就越接近照亮部分。
由于多重采样的平均值相对于单次采样更接近期望深度,因此这个滤波算法也被称为Percentage-Closer Filter
PCF是一种很朴素的思想,带来的问题也很多。
- 首先,多重采样非常影响性能,单次采样的开销取决于GPU是否支持Pre-Fetch Texture和这个采样是否是Simple Texturing(不依赖其他采样结果的采样)。但无论单次采样效率如何,多重采样在算法层面效率就低下。
通过控制多重采样的范围和步长,我们可以控制采样的效率和阴影的总体软硬程度,在相同步长下,一个3x3的PCF不如一个一个5x5的PCF“软”
-
其次,PCF还不能支持pre-filtering(所谓pre-filtering是指在渲染阴影纹理的时候就进行filter滤波处理),无法利用mipmap做完美的三线性插值
-
最后,基于采样的阴影模糊一般都会有二次走样的问题,这是基于sampling的方法无法绕过的问题
效率和存储
存储:32F PCF是是完完全全的非pre-filtering的方法,性能取决于场景复杂度和过滤核的大小,通常来说性能表现较差
Convolution Shadow Maps:卷积阴影
CSM的\(f(d,z)\)表达式为:
$$ f(d,z) \approx \frac{1}{2} + 2\sum_{k=1}^M\frac{1}{c_k}sin[c_k(d-z)] $$
其中 $$ c_k = \pi(2k-1) $$
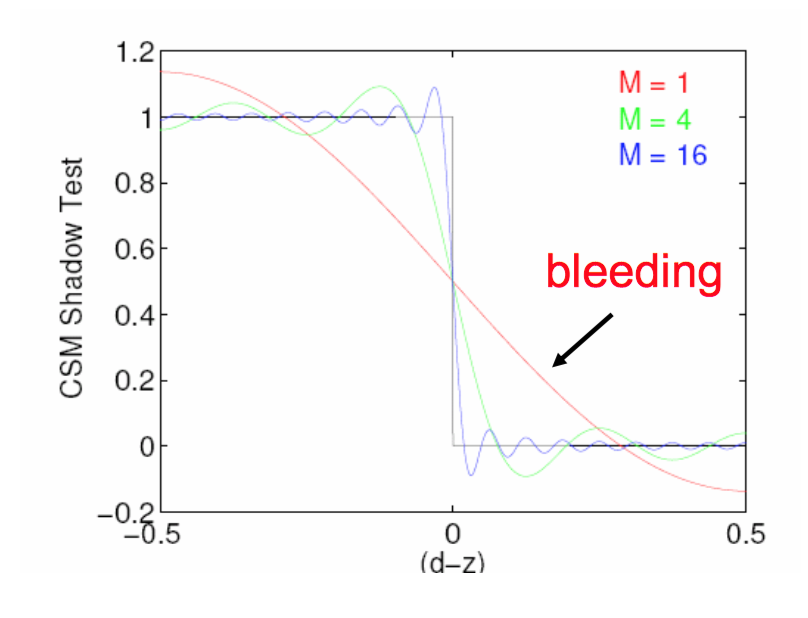
当M取不同的值的时候,\(f(d, z)\)的曲线如下:
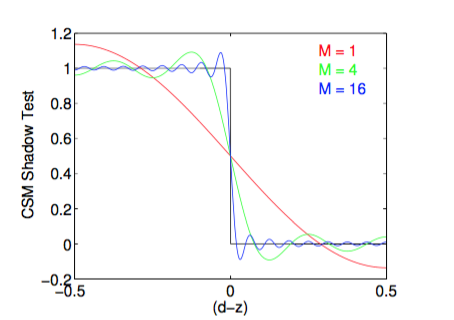
考虑到效率和实现效果,M应该取大于4的值,
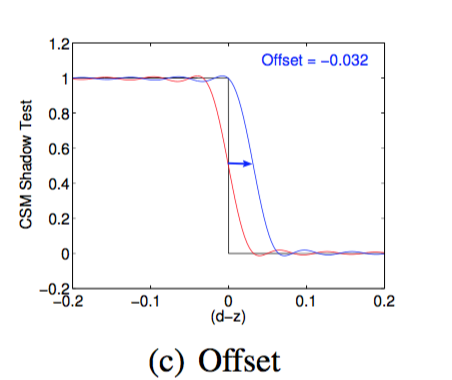
当d=z的时候,\(f(d, z)\)取值0.5,这显然是不对的,因为当d=z,我们应该得到一个完全无遮挡的表面,所以应对原始的函数取一点偏移, 使d=z时\(f(d, z)\)取值1,得到的函数图像如下:
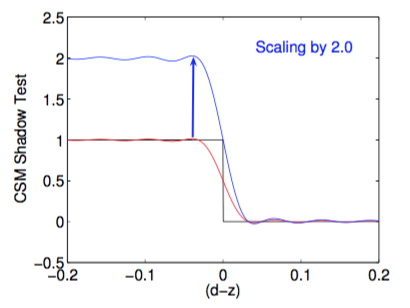
我们也可以对\(f(d, z)\)做一下变形,通过简单的\(f(d, z) \rightarrow 2f(d, z)\),并裁剪超过1的部分, 这样也能得到可以接受的图像
CSM存在的问题
观察CSM的图像,在d=z的两边曲线都出现了抖动,反应在渲染结果上就是物体在和光源连线上的忽明忽暗

抖动和漏光对CSM来说就像双刃剑的两面,要么抖动多一点,要么漏光多一点,
效率和存储
M*(R8G8B8A8) (M \geq 4) CSM支持pre-filtering,M越大,效率越低,但比起PCF来说要好很多
Variance Shadow Mapping: 深度概率分布和切比雪夫不等式
为了分析阴影边缘分布的统计规律,我们考虑光源视角的深度为一个随机变量x。根据切比雪夫不等式的单边公式,深度大于给定值t的概率有一个上界 $$ p(x\geq t) \leq \frac{\sigma^2}{\sigma^2+(t-\mu)^2} $$ 这个上界有多接近于$$p(x\geq t)$$?我们可以假设一个被称为single-bounded的理想模型。
假设把深度为d1的平面投影到深度为d2的平行平面,那么在深度为d1的平面边缘,可以假设投影深度正好为d2的概率为p(这个p也可以认为是pcf的值)那么可以得到深度的期望为 $$ E(x) = pd_2+(1-p)d_1 $$ 而 $$ E(x^2) = pd_2^2+(1-p)d_1^2 $$ 期望的方差: $$ \sigma^2 = E(x^2) - E(x)^2 = (p-p^2)(d_2-d_1)^2 $$ 这样我们就可以根据上面提到的切比雪夫的单边公式来计算深度小于\(d_2\)的上界
$$ P_{max} = \frac{\sigma^2}{\sigma^2+(\mu-d_2)^2} $$ $$ = \frac{(p-p^2)(d_2-d_1)^2}{(p-p^2)(d_2-d_1)^2 + (pd_2 + (1-p)d_1-d_2)^2} $$ $$ = \frac{(p-p^2)(d_2-d_1)^2}{(p-p^2)(d_2-d_1)^2 + (1-p)^2(d_2-d_1)^2} $$ $$ = \frac{p-p^2}{1-p} $$ $$ = p $$
这个结果刚好就是p的值, 这表明,$$P_{max}$$和$$p$$在理想情况下是一样的
虽然这是一种非常特殊的情况,只有一次投影,一个遮挡物,但是这个结果表明,由切比雪夫不等式计算出来的上界很可能只有一点点的偏移,我们可以直接采用这个上界作为阴影测试函数\(f\)
然而,当对VSM应用一个较大核的滤波,也就是像基于VSM生成软阴影的时候,将会导致结果有较大偏差
VSM的实现
VSM的实现关键在于渲染到深度纹理的同时渲染深度的平方,并在shading pass计算期望和方差。这个深度贴图会占用比之前多一倍的内存
实现需要注意几个地方:一是在shadow pass 的时候就利用mipmap,高斯模糊等技术做好预处理,减少锯齿和突变。二是在shading 的时候,注意只有深度大于期望的时候才利用切比雪夫公式进行近似计算(这是由于计算的深度是一个上界)
效率和存储
存储:32+32 VSM同样支持pre-filtering但效率比CSM稳定,开销也更小
Exponential Shadow Mapping
在ESM中,\(s(x)\)的形式是: $$ s(x) = f(d, z) = e^{-c(d-z)} = e^{-cd}e^z $$
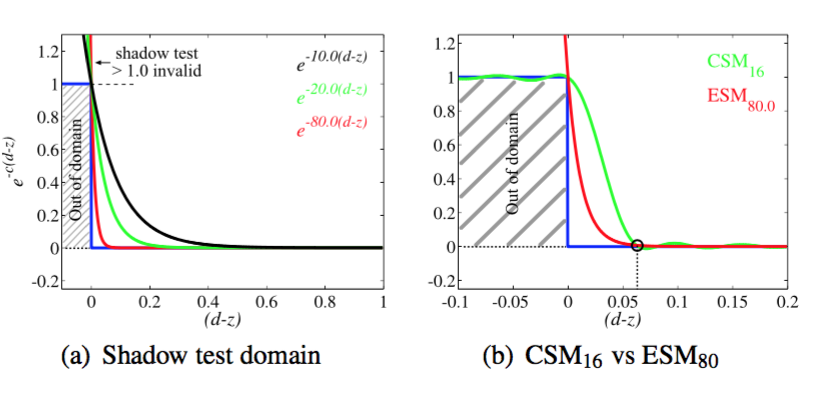
显然这个表达式是单边有效的,对于d<z的情况,$$ e^{-cd}e^z $$ 将会爆炸式增长,我们暂时先假定\(d<z\)时\(f(d, z)=1\)
得到ESM的图像表示:
有了这个表达式,我们就有可能实现pre-filtering,从而提高性能。 下面的式子证明了经过ESM处理之后filtering和pre-filtering是等价的
$$
\begin{align} s_f(x) &= w\ast f(d(x), z) \ &= w\ast (e^{-cd(x)}e^{cz} \ &= e^{-cd(x)}w\ast e^{cz} \ \end{align}
$$
常数指数c的选择会影响ESM的\(s(x)\)曲线:C越大,s(x)越陡峭,也就越接近真实的阴影;当c的值偏小的时候,会造成漏光。 C的上限受到浮点数精度的影响。32位float对应的c的经验最佳值大概在80左右,这个值生成的阴影比\(M=16\)的CSM更好
ESM存在的问题
下面这个图很好的反应了由shadow map精度带来的问题
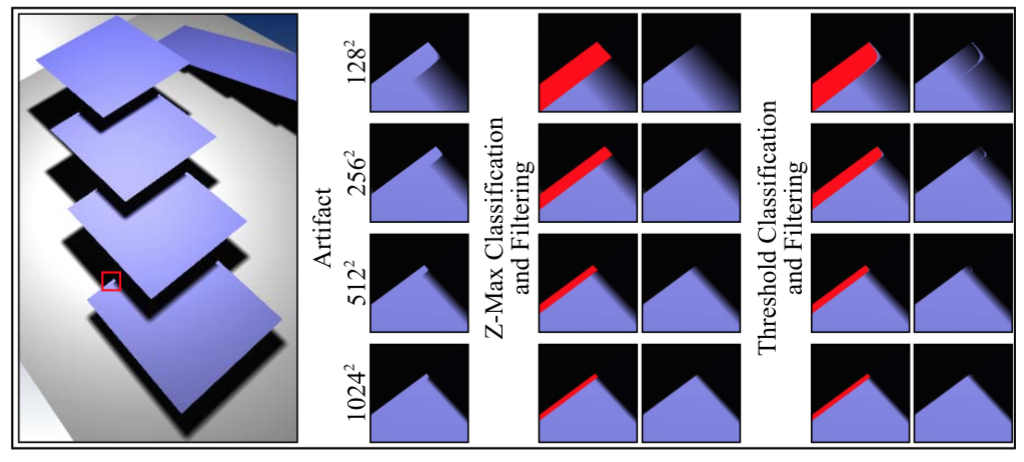
观察图中的边缘,发现有过亮的现象产生,我们用一张图可以清晰明了的解释
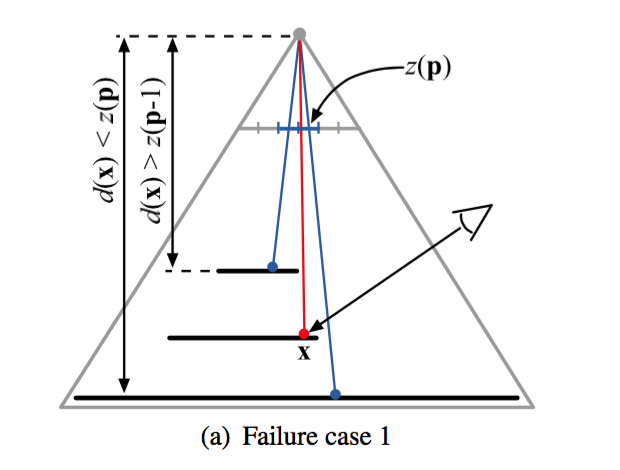
对于阴影纹理,存储和采样点都在纹素中心,当我们计算d(x)-z(p)时就会出现小于0的情况。于是我们得到一个全白的结果,而正确结果应该是有50%的阴影
这种情况出现在多重阴影的边缘,原论文中有两种解决方案,一种是增加一个
$$ Z_{max} $$
的pre-pass,还有一种是对
$$ e^{-cd}e^z $$
设置一个阈值\(1+\sigma\)。这两者都很好理解,
$$ Z_{max} $$
的方法通过找找到附近的最大深度值来判断是否取样到了比d还远的表面,阈值检查\(e^{-cd}e^z\)是否超过某个值,若超过某个值就有可能遇到了上面的情况,就可以对附近的深度做一个PCF来修正采样误差
总的来说,阈值\(1+\sigma\)的效率比Z-max要好,没有多出来的pre-pass,更何况要计算Z_{max}免不了要采样多次,虽然同时阈值的方法不能保证所有的情况,但胜在效率高,存储小。
ESM的实现
ESM只需要一个32F的浮点纹理,存储$$e^{-cd}e^z$$ 的值,之后可以直接对阴影纹理进行线性插值,高斯模糊等操作
存储和效率
:32F ESM比之前提到的几乎所有方法都要好,不需要MRT,支持pre-filtering,没有震荡现象,可以说是最优的方案
PCSS
PCSS是Percentage-Closer Soft Shadows的简称。PCSS和上面的算法解决的是不同的问题。 PCSS解决了前述算法软阴影的一致性问题。原本的滤波算法不管遮挡物和阴影接收物体相距多远,都生成一致的“软”的阴影。
PCSS 通过一个和光源位置相关的相似三角形来控制软阴影的采样搜索范围。下面这个图展示了PCSS如何根据光源,遮挡物,和阴影投射目标三者确定搜索范围
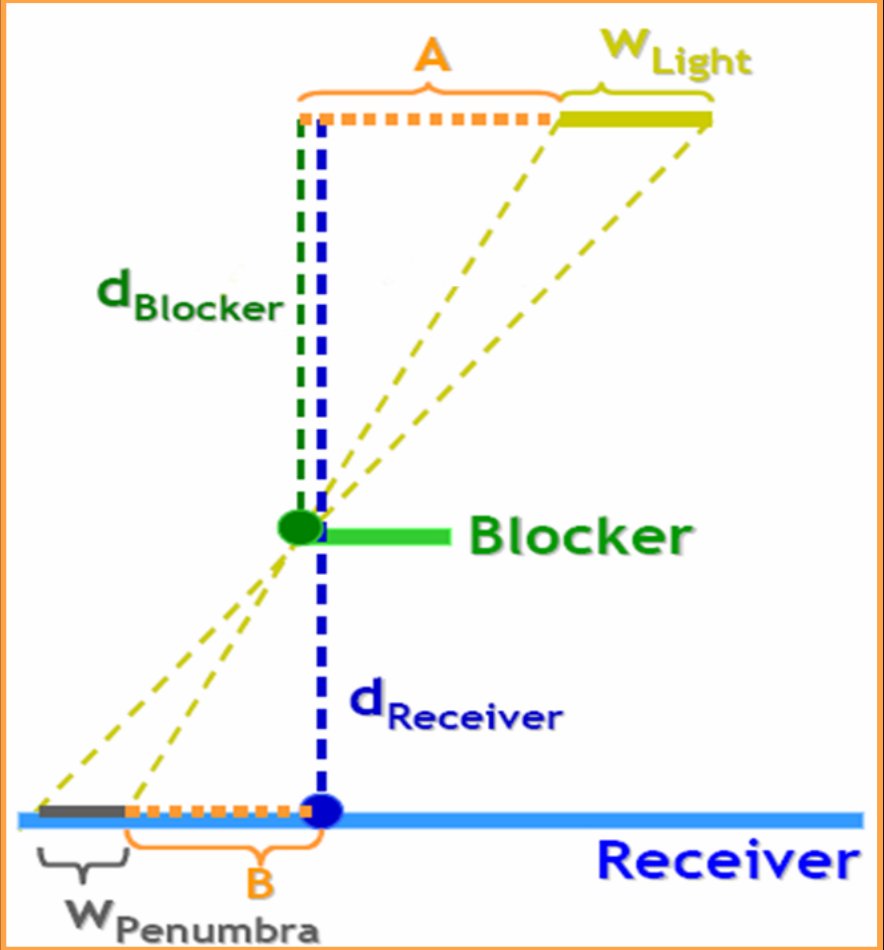
PCSS首先假定光源是一个区域光(area light),这看起来好像很不可思议,但其实这才是我们最常见的光源。 传统的点光源,聚光灯和平行光,其实都不过是某种模拟,比如点光源模拟小灯泡,聚光灯模拟手电筒,平行光模拟太阳,其实严格来说这些都是区域光,软阴影形成的很大一个原因就是区域光的存在。 为了在旧的光源体系中加入区域的概念,我们假定光源是一个始终平行于接收面的圆形,并用uniform变量控制这个圆形的半径 这样,我们就可以估算根据光源,遮挡物,被遮挡物三者的距离估算阴影的软硬程度
计算公式:
$$
W_{Penumbra}=\frac{(d_{Recevier}-d_{Blocker})\dot{w_{Light}}}{d_{Blocker}}
$$
原理非常简单,就是利用了一下三角形的相似性
PCSS的主要贡献在于形成了所谓“动态”的阴影,PCSS确定的这个搜索范围,也可以看做是某种模糊半径,或者卷积核的大小,并没有要求一定按照多重采样(PCF)的方式来实现,因此可以很好地和VSM,ESM等技术结合
参考文献
Fernando, Randima. “Percentage-closer soft shadows.” ACM SIGGRAPH 2005 Sketches. ACM, 2005.
Donnelly, William, and Andrew Lauritzen. “Variance shadow maps.” Proceedings of the 2006 symposium on Interactive 3D graphics and games. ACM, 2006.
Annen, Thomas, et al. “Convolution shadow maps.” Proceedings of the 18th Eurographics conference on Rendering Techniques. Eurographics Association, 2007.
Annen, Thomas, et al. “Exponential shadow maps.” Proceedings of graphics interface 2008. Canadian Information Processing Society, 2008.
Bavoil, Louis. “Advanced soft shadow mapping techniques.” Presentation at the game developers conference. Vol. 2008. 2008.
Shen, Li, Jieqing Feng, and Baoguang Yang. “Exponential soft shadow mapping.” Computer graphics forum. Vol. 32. No. 4. Blackwell Publishing Ltd, 2013.