The original paper:
Paris, Axel, et al. “Terrain Amplification with Implicit 3D Features.” ACM Transactions on Graphics (TOG) 38.5 (2019): 1-15.
近年来，SIGGRAPH 关注隐式建模这种传统领域的的文章越来越少，目前学界的重点主要在研究怎么把深度学习和计算机图形学结合。本文属于少见的关注到隐式建模对于 3D 地形意义的文章。
隐式建模可定义为 求一个3元的隐函数 \( f(x, y, z) = c \) 的解的分段线性近似
Contributions/TOC:
- 一个程序化模型，用以表示地形的地质学性质
- 一个连续的，基于隐表面的地形构造树，支持对地貌的紧凑编码（ 如拱形和山洞）
- 一个高效的的3D地貌生成器，它将会把高度图转化为一个 Implicit 表示，并和其他的 3D Feature 结合
- 一个高效的针对2中的数据结构的多边形化算法（iso 算法）
地质学模型和地形CSG
构造树由两部分构成：
- 一个地质学模型 G，用以表示基岩的分层特性
- 一个隐式表面 T，定义地貌
这两部分都是一个 CSG 树，G 定义了一个地形的阻力场 \( \rho \)。T 定义了等值面为地表的一个标量场
地质学模型 \( G \)
G 的作用在于指导在什么地点生成山洞等破坏性的地形，在 \( G(x, y, z) < 0 \) 的位置这些地形最有可能出现。至于具体生成什么样的地形，可以由用户指定，也可以使用一个预先构造的 CSG 树
G 的基础元素可以来源于湍流（Turbulence）和有分层的地层结构（Strata），经过一些地质力的作用，形成褶皱和断层。最后，由于这些分层结构的对侵蚀的不同抵抗力，地面逐渐形成了不同的侵蚀效果
具体来说，地形对侵蚀的抵抗力可以用一个三维标量场 : \( \rho: \mathbb{R}^3 \rightarrow [0, 1] \) , 表示。0 和 1 分别表示最大最小的阻力值
湍流（Turbulence）
湍流可分为
- 全方向的: \( \rho(p) = t(p/\lambda_0) \)
- 仅垂直方向: \( \rho(p) = t(p_z/\lambda_0) \)。
全方向的湍流生成混乱的地形，可简单应用 Simplex Noise, 或者应用 FBM 中的 Wrap 。 垂直方向的湍流和下面的底层搭配能形成褶皱（Fold）效果
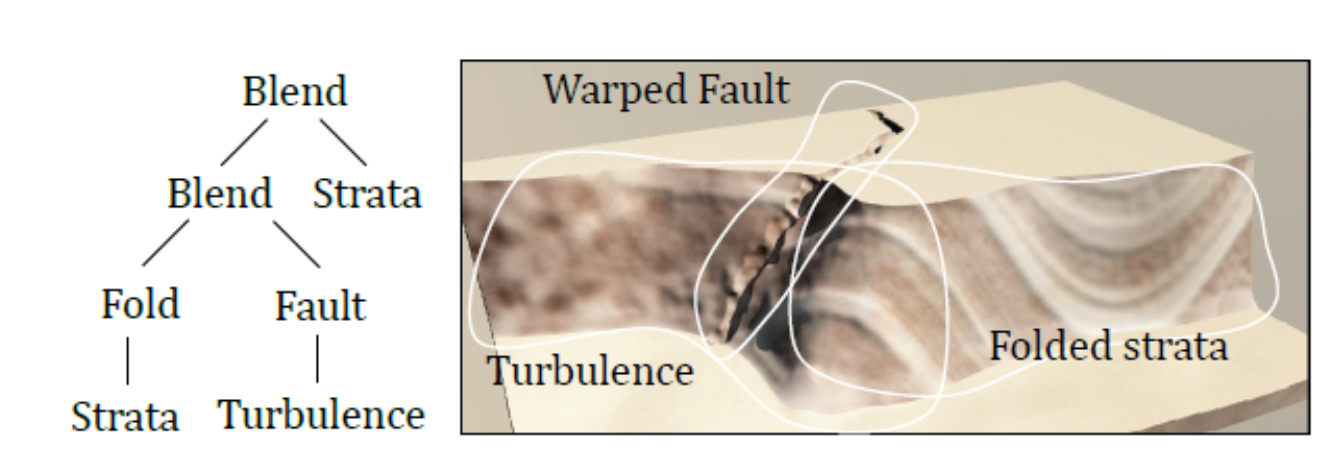
地层（Strada）
为了表示地层结构（Strada），需要生成在垂直高度上统一变化的阻力场，本文 通过组合 平面 SDF 加上一个衰减函数来做到 ： \( \rho(p) = g \circ d(p) \)
d 是 plane SDF，g 即是衰减函数， t 是加入的湍流（Turbulence Noise）扰动
隐表面 \( \mathcal{T} \)
该论文所描述的 Terrain Implicit function 实际也只是 把 高度函数 \( h(p_{xy}) \) 转换为一个3D 的隐式函数
$$ f_\mathcal{T}(p) = \sigma \circ \nu(p) $$
其中 $$ v(p) = h(p_{xy}) -p_z $$ 这个就是一般的高度场直接转换为隐式表示的的最简单做法。但作者又对其做了进一步的处理
$$ \sigma (x) = \begin{cases} T+x+\frac{3T-2R}{R^2}x^2+\frac{R-2T}{R^3}x^3 &, 0<x<R \\\ 2T &, otherwise \end{cases} $$
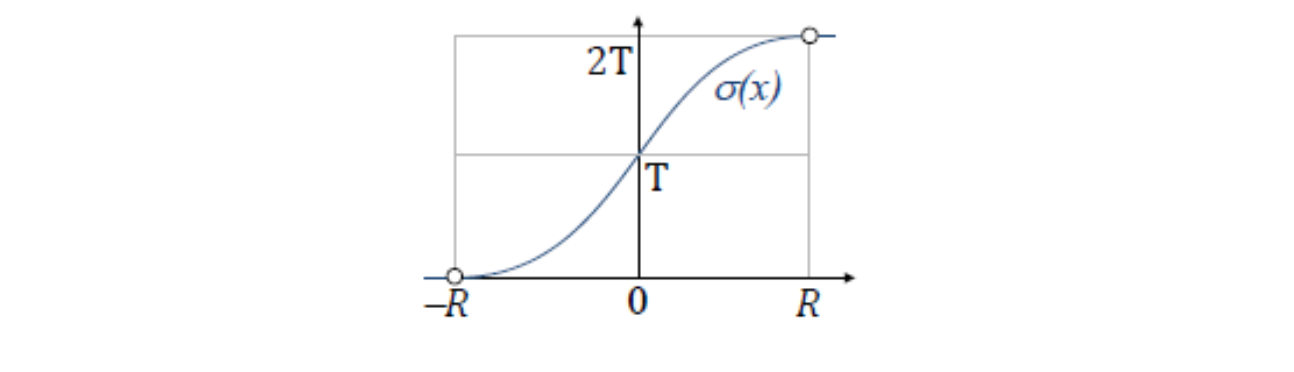
此处理的作用为使得距离地面超过R的位置不受地形的影响。（这个处理带来的明显问题是使得 \( \mathcal{T} \) 的局部性增强，不利于 LOD 和 SDF Culling ）
接下来就是作者要引入的 3D Feature 部分了。这个思路也是和传统 CSG 和 SDF 操作 相似，通过 Union / Subtract 另一个 CSG \( \mathcal{S} \) 来制造山洞和悬崖等效果。
造浮岛的思路也和我想的一样：对两个 Terrain 做 Intersection，其中一个做了旋转/镜像
多边形化算法
本文举例了四个特征地形，每个地形的节点个数都上万了
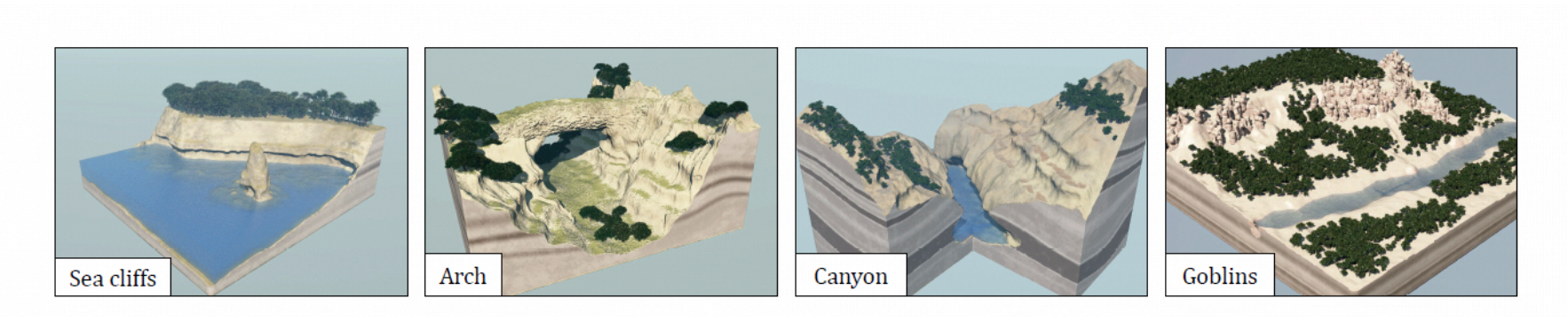
这就导致 Evaluating implicit value 代价过大，因此他们的优化重点还是减少 Eval 的调用
优化1: Narrow Band of MC Cells
他们利用了只是对 Terrain 进行局部修改的特性，这样就非常适合加速 ISO point 的寻找过程以及 seed 类算法的应用。具体实现中该文 Query 了 Height Field 输入地形的一个 Narrow band
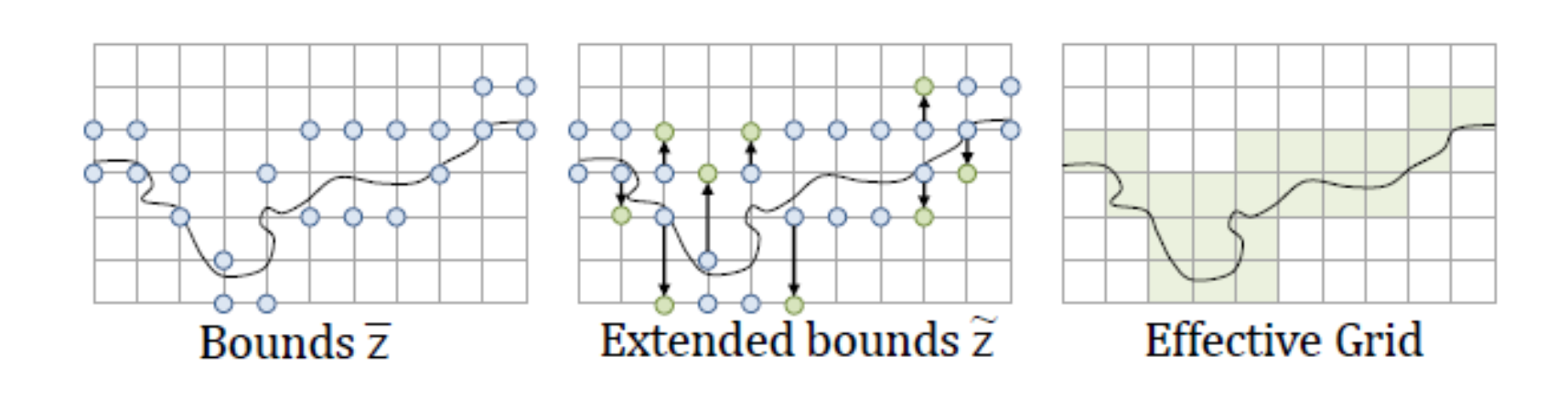
为了寻找这个 Narrow Band 实际上需要每个节点定义一个 Z Interval 函数 \(（minZ, maxZ）= z(x, y) : \mathbb{R}^2 \rightarrow \mathbb{Z}^2 \) ：输入一个 二维坐标，返回这个节点在 Z 方向上 Implicit Value 小于 0 的 Bound (离散化的) 。对于高度图很简单 \( minZ=maxZ=h(x, y) \) , 对于基本元素如 sphere，可以取到 analytical 的 bound，或者直接返回 BoundingBox 的 Z Interval。
为了保证 最后的 Mesh 是一个 \( C^0 \) 连续函数，还需要对 这个 Interval 做一次扩张，文中的方法是把每个 Interval 和附近的 1环邻域合并，使得每个 Interval 之间是连续的
总结：根据表格数据，这个优化最大提速 12 倍左右 （相比于标准 Marching Cubes）
优化2：Direct Elevation of Height Field
直接用高度/高度的线性插值来生成 Vertex，这个优化只有 1.5-2.5 的提速，有点奇怪
本文的优化效率依赖于真 3D Feature 占据地形的比重，比重越高优化效率越低（趋近于标准 Marching Cubes）